Ingenuity’s Early Modern Campaign against Uncertainty: Bridging the Gap between the History of Art and Science
Acting individually or collectively, human ingenuity is able to adapt to rapid,complex change. With increased population density, and the burden we have placed onour natural environment, society must cope with more complex, and often unpredictable circumstances, requiring ever increasing amounts of ingenuity to manage our relationship with the world (Homer-Dixon). How much, and what kind of ingenuity should be used depends on a range of factors including society’s goals and the framework within which those goals must be achieved. But is there a right kind of ingenuity? That we can no longer predict the behavior of complex systems with precision implies that ingenuity should be practiced in order to make sense of the future, not the present. During the
sixteenth century ingenuity was praised for its ability to solve technical and social problems, but it was also idealistic. Comparing the architect to an engineer in the last sentences of his Dieci libri dell’architettura (1567), Venetian patrician Daniele Barbaro recalls a famous proverb that sums up the importance of ingenuity to the architect. Barbaro advises that his treatise “ought to be diligently considered by every engineer, because one often finds truth in that proverb which says, ingenuity overcomes the forces of nature.” (482) As an example, Barbaro proffers the Verona Bridge, which is able to withstand the weight of carriages as well as the waters of the Adige River, because of the action taken by ingenious architects. In this book I explore the temporality of early modern ingenuity, focusing on how ingenuity became conceptualized as preventative in nature, encompassing matters of prognosis and forecast directed at overcoming uncertainty.
Whether artistic or scientific, there are ideals associated with the wider meaning and purpose of ingenuity. The word ingenuity is derived from the Latin ingenium, which broadly denotes “intellectual power” (Klein). For the sixteenth-century Italian architect, ingenuity, or ingegno, stood for the ability to conceive of architectural designs, as well as the mathematical skill required to realize such achievements (Lewis). Ingegno was, above all, a virtue, through its ability to judge, and while it was not something that could be learned, it could be developed and exploited with the help of other virtues (Syson and Thornton). What has yet to be fully explored is how ingenuity was often temporally conditioned by prudence. In his Paradiso, Dante insists the virtue that perfects ingegno is prudence (Dumol). Described as the practical reason that guides our choices when making conscious decisions that affect the future (Summers), prudence is temporally determined. In this study, I consider the link between ingenuity and prudence in the framework of what Lorraine Daston and Peter Galison refer to as “epistemic virtues,” norms that are internalized and administered in an appeal to ethical values as well as the securing of knowledge.
My research has been attentive to how ingenuity acquired a temporal component in sixteenth-century architectural theory, through its relationship to prudence. In response to the devastation endured by his native city of Vicenza during the wars of the League of Cambrai, Giangiorgio Trissino incorporated prudence as a primary component of ingegno in his epic poem, Italia liberata dai Goti. Lacking illustrations – aside from a map by Andrea Palladio, drawing attention to the principal architectural sites of Rome – the work presents the poetic experience of architecture through its narrative. Relying on ingenuity and prudence, one of the principal characters, Callidio, constructs mills on the locations on the Tevere where the Goths destroyed the aqueduct, reinstating the water source for the Italian people and putting the aqueduct to better use by providing facilities to mill grain and help feed the nation. Callidio’s use of a democratized type of prudence that takes advantage of present conditions to make improvements provides proof of his commander Belissario’s counsel that “ingenuity is mightier than force.” While the additions to the aqueduct would benefit the future population, prudence is not used here in the Machiavellian sense, which tries to satisfy the way our desires of future unknowns play out (Mansfield). The value of Trissino’s work as part architectural treatise has never been given the attention it deserves. I begin my study by scrutinizing Trissino’s work in order to reconstruct the broader field of ingegno as it was used in humanist philosophy, poetics and architectural theory.
While there is a similarity between Belissario’s advice in Trissino’s poem and the proverb cited previously by Barbaro, by comparing the architect to an engineer Barbaro’s use of ingenuity marks a semantic shift. Increasingly, as architectural training became ever more associated with mathematics, architects began to identify themselves more exclusively as engineers, or ingegnieri (Lefèvre). Ingenious new fortifications built to withstand cutting-edge weaponry were often referred to as machines, or macchine. I continue by exploring ingenuity’s imperative to predetermine future outcomes in the Tenth Book of Barbaro’s Dieci libri, where he considers the architectural design of machines such as watermills, and mechanisms of war. This section will focus on how the consequences of war resulted in strategies to control the damages of time through a newly governed ingenuity.
When the requirements for the formation of a successful architect are categorized in the Dieci libri, ingenuity tops the list, but the problem solving inherent in architectural practice is a matter of judgment, which pertains to prudence (12). “Judgment,” Barbaro writes, “is a matter of prudence; prudence compares preceding things with the moments, and evaluates things to come.” Guided by his definition of prudence as it relates to ingenuity, in my dissertation I examine how the algorithmic nature of prudence – where subsequent evaluations are dependent on preceding ones – permeated the relationship between different parts of the structure of Barbaro’s Villa Maser, generating a prescriptive configuration of space aimed at vanquishing the destructive effects of time. Barbaro’s esteem for ingenuity’s ability to triumph over future uncertainty has its roots in the primacy of number. In the Renaissance, the debate over the superiority of number over line was rooted in the opposition between the ‘Pythagorean theory of numbers’ and the ‘Euclidean geometry of lines,’ a polarity which, Michele Sbacchi observes, was manifest most prominently within the theory of architecture. Barbaro’s declaration that architecture should be “transformed to include two sciences, both natural and mathematical” highlights an attempt to unite these two discordant systems of knowledge under a single comprehensive umbrella.
The source for Barbaro’s interest in the numerical component of mathematics was Proclus’s Commentaries on Euclid. The importance of number to Proclus’s commentaries cannot be overemphasized, and Barbaro championed this feature when it came to solving geometrical problems. In the Dieci libri, Barbaro insists that what is useful to the architect is “arithmetic’s ability to demonstrate reasons for measurement, and to dissolve uncertainties which, for geometry, are unsolvable.” (15) While geometric drawing was an essential component of architectural practice, the revival of Euclidism, Sbacchi contends, must be accredited to Francesco Barozzi, and by extension Barbaro his pupil, to whom he dedicated his Opusculum with the assertion that “the certitude of mathematics is contained in the syntactic rigor of demonstrations.” I continue my study by fleshing out how the immateriality of number was used to solve the problems of speculative geometry in the Dieci libri, with the hope of demonstrating architecture’s role in erasing the slippery boundary between number and geometry in the Renaissance, and the profound impact this had on the history of science.
My research reveals how the importance of angular notation to solving geometrical problems was developed by Barbaro to create a new way of putting two-dimensional objects in perspective, a conception directed by the authority of prudence, and first developed in his treatise to makes provisions for the movement of light through space as a critical component of representation. The confluence of prudence and space was determined by the science of constructing sundials. Barbaro’s theoretical dependence on the gnomon – the projecting piece on a sundial that shows the time by the position of its shadow – is evident from his definition of one of the three components that define architecture as a practice: Gnomonica. When it comes to this section, “nothing is of use to the architect, unless we wish to find some secret quality of location, the discernment of which can only refer to the order and influence of the planets.” (20) Barbaro delineates how the production of shadows will change depending on the shape of the surface on which the shadow is projected, and here he argues how with the help of perspective, it is possible to design the effects on a building, which one can read like an analemma, and from which one can even determine in which sign of the zodiac the sun is positioned. Barbaro draws on prudence’s algorithmic nature, noting how the degree of every subsequent shadow is dependent on the shadow that precedes it, a notation that may be seen as a precondition for logarithmic functions.
The use of angular notation for putting objects in perspective was developed to a considerable extent by Albrecht Dürer, who Barbaro praises for his ingenuity in his Pratica della perspettiva (1569). Dürer’s Underweysung der messung mit dem zirckel un richt scheyt (1525) illustrates how objects in space are dependent on a perspectival system based on the circularity of the sun’s rays, illustrating how degrees, minutes and seconds became an intrinsic part of that construction. The use of number, as angular notation, is translated from the protractor-like semicircle marked with degrees along the curved edge, to the vertical axis on the right. The radius of the circle serves as a horizontal axis, and together the two axes bear a strong resemblance to the Cartesian coordinates developed later. Angular notations are laid out numerically, and linearly like an algorithmic series. The relationship between the angle used to delineate the object’s position and its distance from the radius is determined by the sine function. My independent research has uncovered how Alberti’s construction of linear perspective can be duplicated using a plot of the natural logarithm y = lnx, by extending a line perpendicular to the y axis at the value for the limit of the natural logarithmic function, e = 2.7187, that represents the horizon. In algebra, the limit of a function is a measure for reducing the uncertainty of infinity to a finite number. Though it wasn’t until the middle of the eighteenth century that the correlation between the sine function and the natural logarithm was drawn, John Napier’s Logarithmorum Canonis Descriptio (1616) establishes a similar relationship. The measurements for his calculations depend on a system using an angular notation of minutes, which begin at 0 and end at 60, like Dürer’s illustration, and Napier likely derived his calculations from sources discovered on his trip to Venice (Napier). It is well known that the invention of the logarithm was foreshadowed by the comparison of the arithmetic and geometric series, but the role played by artistic developments in perspective have yet to be explored. Focusing on the treatises of Dürer and Barbaro, this book explore how prudence shaped ingenuity’s push to limit uncertainty, in order to test the relationship between Napier’s logarithmic calculations and linear perspective further.
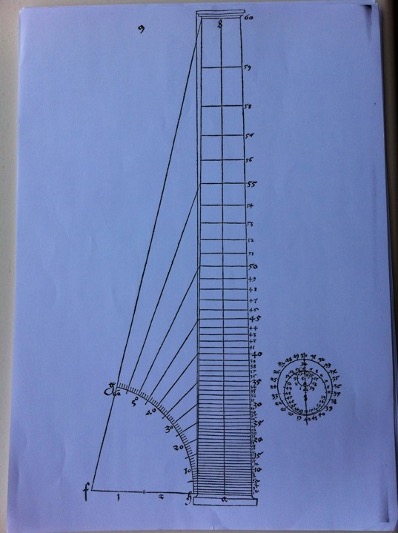
Underweysung der messung mit dem zirckel un richt scheyt, Albrecht Dürer, 1525, p. 9
Bibliography:
Barbaro, Daniele. I dieci libri dell’architettura di M. Vitruvio, tradutti et commentati da
monsignor Barbaro eletto patriarca d’Aquileggia, In Vinegia: per Francesco Marcolini,
1556.
Barbaro, Daniele. I dieci libri dell’architettura di M. Vitruvio, tradutti et commentati da
monsignor Barbaro eletto patriarca d’Aquileggia, In Vinegia: per Francesco Marcolini,
1567.
Barbaro, Daniele. La pratica della perspettiva, In Venetia: appresso Camillo & Rutilio
Borgominieri fratelli, al segno di S. Giorgio, 1569.
Carpo, Mario. “Drawing with Numbers: Geometry and Numeracy in Early Modern
Architectural Design,” Journal of the Society of Architectural Historians, 62:4, (Dec.,
2003), 448-469.
Cellauro, Louis. “Daniele Barbaro and Vitruvius: The Architectural Theory of a
Renaissance Humanist and Patron,” Papers of the British School at Rome, Vol. 72,
(2004), 293-329.
Daston, Lorraine and Peter Galison, Objectivity, New York: Zone Books, 2010, 41.
Dumol, Paul Arvisu. The metaphisics of reading underlying Dante’s Commedia: The
ingegno, New York: P. Lang, 1998, 126.
Dürer, Albrecht. Clarissimi pictoris et geometrae, Nuremburg: Hieronymum
Formschneyder, 1532.
Field, J. V. “Renaissance mathematics: diagrams for geometry, astronomy and music,”
Interdisciplinary Science Reviews, 2004, Vol. 29, No. 3, 259-277, (263).
Homer-Dixon, Thomas. The Ingenuity Gap, New York: Knopf, 2000, p. 13.
Iversen, Margaret. “The Discourse of Perspective in the Twentieth Century: Panofsky,
Damisch, Lacan,” Oxford Art Journal, 28.2, 2005, 191-202.
Kahn, Victoria. Rhetoric, Prudence, and Skepticism in the Renaissance, Cornell
University Press: London, 1985.
Klein, Jürgen. “Genius, Ingenium, Imagination: Aesthetic Theories of Production from
the Renaissance to Romanticism,” in The Romantic Imagination: Literature and Art in
England and Germany, ed. Frederick Burwick and Jürgen Klein, Amsterdam: Rodopi,
1996, 19-62, (31).
Laven, P. J.. Daniele Barbaro, Patriarch Elect of Aquileia, with special reference to his
circle of scholars and literary achievements, thesis submitted for Ph. D. degree in
History, (London: University, 1983).
Lefèvre, Wolfgang. Picturing Machines, 1400-1700. Cambridge: MIT Press, 2004, 148.
Lewis, Rhodri. “Francis Bacon and Ingenuity,” Renaissance Quarterly, Vol. 67, No. 1.
(Spring, 2014), 113-163, (123).
Lienhard, John H. The Engines of our Ingenuity: An Engineer Looks at Technology and
Culture, Oxford ; New York : Oxford University Press, 2000, p. 10.
Mansfield, Harvey C. Machievelli’s Virtue, Chicago: University of Chicago Press, 1996.
Marr, Alexander. Between Raphael and Galileo: Mutio Oddi and the mathematical
culture of late Renaissance Italy, Chicago: University of Chicago Press, 2011.
Morsolin, Bernardo. Giangiorgio Trissino, Vicenza: Gir. Burato, 1895.
Napier, John. Logarithmorum Canonis Descriptio, seu arithmeticarum supputationum
mirabilis abbreuiatio, Lugduni: apud Barth. Vincentium, 1620.
Napier, Mark. Memoirs of the Marquis of Montrose, Edinburgh: Hamilton, Adams & Co.,
1856, p. 820.
Pacey, Arnold. The Maze of Ingenuity: Ideas and Idealism in the Development of
Technology, London: A. Lane, 1974.
Rose, Paul Lawrence. “A Venetian Patron and Mathematician of the Sixteenth Century:
Francesco Barozzi (1537-1604), Studi veneziani, N.S. 1, (1977), 119-187, (124-126).
Sbacchi, Michele. Euclidism and Theory of Architecture, Nexus Network Journal, Vol. 3,
No. 2 (2001), 25-38, (27).
David Summers. The Judgment of Sense: Renaissance Naturalism and the Rise of
Aesthetics, Cambridge: Cambridge University Press, 1987.
Syson, Luke and Dora Thornton. Objects of Virtue: Art in Renaissance Italy, Los
Angeles: Getty Publications, 2001, p. 135.
Tafuri, Manfredo. “La norma e il programma: il Vitruvio di Daniele Barbaro,” in
Vitruvio: I dieci Libri dell”Architettura, tradotti et commentate da Daniele Barbaro,
1567, ed. Manfredo Tafuri and Mansuela Morresi, Milan, 1987.
Trissino, Giangiorgio. Italia liberata dai Goti, Libro Primo (Londra: Si vende in Livorno
Presso Gio. Tomo. Masi e Comp., 1779), p. 123.
Trissino, Giangiorgio. Scritti scelti, a cura di Attilio Scarpa, Vicenza: Officina
Tipografica Vicentina G. Stocchiero, 1950.